解不等式
已知函数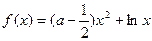 (
(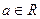 )。
)。
(Ⅰ)当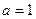 时,求
时,求 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数 的图象恒在直线
的图象恒在直线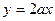 下方,求
下方,求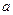 的取值范围。
的取值范围。
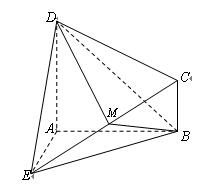
如图所示的几何体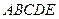 中,
中,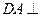 平面
平面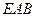 ,
, ,
,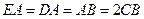 ,
,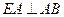 ,
, 是
是 的中点。
的中点。
(Ⅰ)求证: ;
;
(Ⅱ)设二面角 的平面角为
的平面角为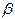 ,求
,求 。
。
已知点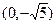 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为 ,椭圆的左右焦点分别为F1和F2 。
,椭圆的左右焦点分别为F1和F2 。
(Ⅰ)求椭圆方程;
(Ⅱ)点M在椭圆上,求⊿MF1F2面积的最大值;
(Ⅲ)试探究椭圆上是否存在一点P,使 ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。
甲、乙等五名亚运志愿者被随机地分到 四个不同的赛场服务,每个赛场至少有一名志愿者。
四个不同的赛场服务,每个赛场至少有一名志愿者。
(Ⅰ)求甲、乙两人同时参加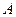 赛场服务的概率;
赛场服务的概率;
(Ⅱ)求甲、乙两人不在同一个赛场服务的概率;
(Ⅲ)设随机变量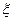 为这五名志愿者中参加
为这五名志愿者中参加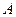 赛场服务的人数,求
赛场服务的人数,求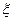 的分布列。
的分布列。
在数列 中,
中, ,
, ,且
,且 (
(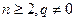 )。
)。
(Ⅰ)设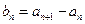 (
( ),求数列
),求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的通项公式。
的通项公式。