某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在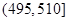 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.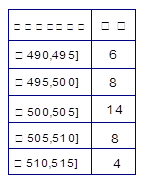

表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面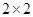 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| |
甲流水线 |
乙流水线 |
合计 |
| 合格品 |
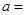 |
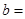 |
|
| 不合格品 |
 |
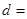 |
|
| 合 计 |
|
|
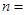 |
附:下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
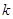 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员 人(140<
人(140< <420,且
<420,且 为偶数),每人每年可创利
为偶数),每人每年可创利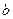 万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利
万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利 万元,但公司需付下岗职员每人每年
万元,但公司需付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
万元的生活费,并且该公司正常运转所需人数不得小于现有职员的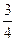 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
定义在R上的单调函数f(x)满足f(3)=log 3且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;(2)若f(k·3
3且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;(2)若f(k·3 )+f(3
)+f(3 -9
-9 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
设关于x的函数f(x)=-1-2a+2cos2x-2acosx的最小值为g(a).(1)写出g(a)的表达式;(2)当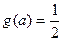 时,求a的值,并求此时f(x)的最大值。
时,求a的值,并求此时f(x)的最大值。
已知幂函数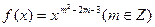 为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数
为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数 的奇偶性。(10分)
的奇偶性。(10分)
(本小题满分12分)
定义在D上的函数 ,如果满足:对任意
,如果满足:对任意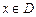 ,存在常数
,存在常数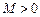 ,都有
,都有 成立,则称
成立,则称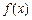 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数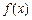 的上界.
的上界.
已知函数 ;
; .
.
(1)当a=1时,求函数 在
在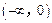 上的值域,并判断函数
上的值域,并判断函数 在
在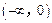 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以3为上界的有界函数,求实数a的取值范围;
上是以3为上界的有界函数,求实数a的取值范围;
(3)若 ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求 的取值范围.
的取值范围.