(本小题满分10分) 选修4—1:几何证明选讲
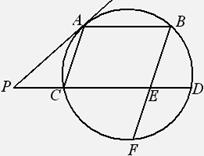
如图,四边形ABCD内接于⊙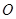 ,过点A作⊙
,过点A作⊙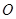 的切线EP交CB的延长线于P,已知
的切线EP交CB的延长线于P,已知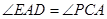 .
.
证明:(Ⅰ)AD=AB;(Ⅱ)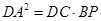 .
.
为备战2012年伦敦奥运会,爾家篮球队分轮次迸行分项冬训.训练分为甲、乙两组,根据经验,在冬训期间甲、乙两组完成各项训练任务的概率分别为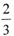 和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
(I)若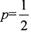 求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
(II)设在6轮冬训中,甲、乙两组成为“友好组”的次数为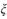 ,当
,当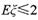 时,求P的取值范围.
时,求P的取值范围.
已知向量
 函数
函数 且最小正周期为
且最小正周期为 .
.
(I)求函数 的最大值,并写出相应的X的取值集合;
的最大值,并写出相应的X的取值集合;
(II)在 中,角A,B, C所对的边分别为a, b,c,且
中,角A,B, C所对的边分别为a, b,c,且 ,c=3,
,c=3, ,求b的值.
,求b的值.
选修4-5:不等式选讲
已知 ,
, .
.
(1)求证: ,
, ;
;
(2)若 ,求证:
,求证: .
.
选修4-4:坐标系与参数方程
已知直线 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
.
(1)求圆心C的直角坐标;
(2)由直线 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
选修4—1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.