小杰到学校食堂买饭，看到A、B两窗口前面排队的人一样多(设为a人，a＞8），就站在A窗口队伍的后面，过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人．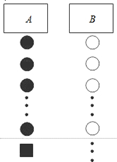
（1）此时，若小杰继续在A窗口排队，则他到达窗口所花的时间是多少？（用含a的代数式表示）
（2）此时，若小杰迅速从A窗口队伍转移到B窗口后面重新排队，且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少，求a的取值范围．（不考虑其它因素）
已知，如图1，△ABC中，BA=BC，D是平面内不与A、B、C重合的任意一点，∠ABC=∠DBE，BD=BE。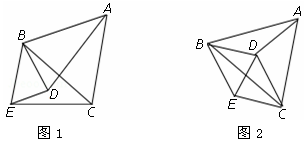
（1）求证：△ABD≌△CBE；
（2）如图2，当点D是△ABC的外接圆圆心时，请判断四边形BDCE的形状，并证明你的结论。
某工厂计划为学校生产A，B两种型号的学生桌椅500套，以解决1254名学生的学习问题，一套A型桌椅（一桌两椅）需木料0.5m3，一套B型桌椅（一桌三椅）需木料0.7m3，工厂现有库存木料302m3。
（1）有多少种生产方案？
（2）现要把生产的全部桌椅运往学校销售，已知每套
型桌椅售价150元，生产成本100元，运费2元；每套
型桌椅售价200元，生产成本120元，运费4元，求总利润
（元）与生产型桌椅
（套）之间的关系式，并确定总利润最少的方案和最少的总利润。（利润
售价－生产成本－运费）
（3）按（2）的方案计算，有没有剩余木料？如果有，请直接写出用剩余木料再生产以上两种型号的桌椅，最多还可以为多少名学生提供桌椅；如果没有，请说明理由。
如图，OA、OB的长分别是关于x的方程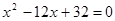
的两根，且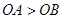
。请解答下列问题：
（1）求直线AB的解析式；
（2）若P为AB上一点，且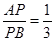
，求过点P的反比例函数的解析式。
如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，∠BFQ＝60°，EF＝1km。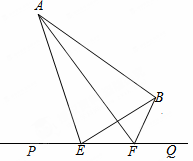
（1）判断AB、AE的数量关系，并说明理由；
（2）求两个岛屿A和B之间的距离（结果精确到0.1km）。（参考数据：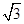
≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3. 49，sin76°≈0.97，cos76°≈0.24）
如图，已知△ABC，且∠ACB＝90°。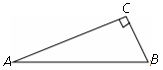
（1）请用直尺和圆规按要求作图（保留作图痕迹，不写作法和证明）
①以点A为圆心，BC边的长为半径作⊙A；
②以点B为顶点，在AB边的下方作∠ABD=∠BAC。
（2）请判断直线BD与⊙A的位置关系。