如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，∠BFQ＝60°，EF＝1km。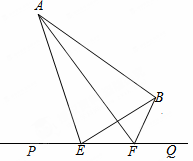
（1）判断AB、AE的数量关系，并说明理由；
（2）求两个岛屿A和B之间的距离（结果精确到0.1km）。（参考数据：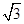
≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3. 49，sin76°≈0.97，cos76°≈0.24）
如图，甲、乙两座建筑物的水平距离 为 ，从甲的顶部 处测得乙的顶部 处的俯角为 ，测得底部 处的俯角为 ，求甲、乙建筑物的高度 和 （结果取整数）．参考数据： ， ．
已知 是 的直径，弦 与 相交， ，
如图①，若 为 的中点，求 和 的大小；
（Ⅱ）如图②，过点 作 的切线，与 的延长线交于点 ，若 ，求 的大小．
某养鸡场有2500只鸡准备对外出售，从中随机抽取了一部分鸡，根据它们的质量（单位： ，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：
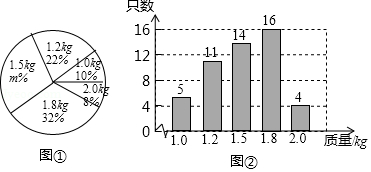
图①中 的值为 ；
（Ⅱ）求统计的这组数据的平均数、众数和中位数；
（Ⅲ）根据样本数据，估计这2500只鸡中，质量为 的约有多少只？
解不等式组
请结合题意填空，完成本题的解答．
解不等式①，得 ；
解不等式②，得 ；
（Ⅲ）把不等式①和②的解集在数轴上表示出来；
（Ⅳ）原不等式组的解集为 ．
已知抛物线 是常数）经过点 ．
（1）求该抛物线的解析式和顶点坐标；
（2） 为抛物线上的一个动点， 关于原点的对称点为 ．
①当点 落在该抛物线上时，求 的值；
②当点 落在第二象限内， 取得最小值时，求 的值．