如图,已知函数y=﹣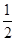 x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣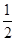 x+b和y=x的图象于点C、D.
x+b和y=x的图象于点C、D.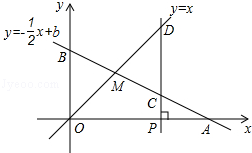
(1)求点A的坐标;
(2)若OB=CD,求a的值.
现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
| 运往甲地(单位:吨) |
运往乙地(单位:吨) |
|
| A |
x |
|
| B |
(2)设总运费为W元,请写出W与x的函数关系式.
(3)怎样调运蔬菜才能使运费最少?
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)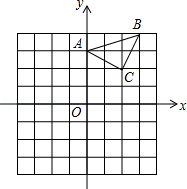
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)作出△ABC关于原点O成中心对称的△A3B3C3,并直接写出B3的坐标.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.(提示:将△AED绕D点按逆时针方向旋转90°,得到△A1FD,把阴影部分构造成规则的图形)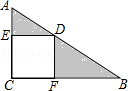
直线l与直线y=2x+1的交点的横坐标为2,与直线y=﹣x+2的交点的纵坐标为1,求直线l对应的函数解析式.