如图1,四边形 内接于 , 是 的直径,过点 的切线与 的延长线相交于点 .且
(1)求证: ;
(2)过图1中的点 作 ,垂足为 (如图 ,当 , 时,求 的半径.

如图,在平面直角坐标系中,直线y=0.5x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,过点D作DE⊥x轴,垂足为E.
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.
已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y= x的图象相交于点(2,m).
x的图象相交于点(2,m).
(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
| A型利润 |
B型利润 |
|
| 甲店 |
200 |
170 |
| 乙店 |
160 |
150 |
(1)设分配给甲店A型产品x件,这件公司卖出这100件产品的总利润W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若要求总利润不低于17560元,有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A、B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大.
如图,已知△ABC的三个顶点在格点上.
(1)作出△ABC关于x轴对称的图形△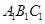
(2)求出△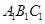 的面积.
的面积.
已知2x-y的平方根为±4,-2是y的立方根,求-2xy的平方根.