甲、乙两观光船分别从 、
、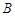 两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达
两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达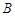 港.下图表示甲观光船距
港.下图表示甲观光船距 港的距离
港的距离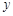 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,结合图象解答下列问题:
(小时)之间的函数关系式,结合图象解答下列问题: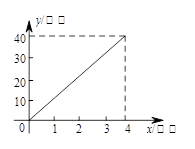
(1) 、
、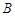 两港距离 千米,船在静水中的速度为 千米/小时;
两港距离 千米,船在静水中的速度为 千米/小时;
(2)在同一坐标系中画出乙船距 港的距离
港的距离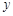 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象;
(小时)之间的函数图象;
(3)求出发几小时后,两船相距5千米.
宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?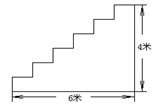
先把下列各数在数轴上表示出来,再用“<”把这些数从小到大排列起来.
3.5,-(-2)2,-1,-2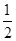 ,
,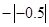
将下列各有理数填入相应的集合内:
整数:{ …}负分数:{ …}
正数:{ …}负数:{ …}
如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒
2cm的速度沿折线A—C—B向点B运动,设运动时间为t秒(t>0),
(1)在AC上是否存在点P使得PA=PB?若存在,求出t的值;若不存在,说明理由;
(2)若点P恰好在△ABC的角平分线上,请直接写出t的值.
如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1, l2,l3之间的距离为2 ,点A、C分别在直线l2,l1上,
(1)利用直尺和圆规作出以AC为底的等腰△ABC,使得点B落在直线l3上(保留作图痕迹,不写作法);
(2)若(1)中得到的△ABC为等腰直角三角形,求AC的长.