如图,在平面直角坐标系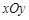 中,
中,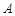 、
、 为
为 轴上两点,
轴上两点,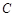 、
、 为
为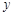 一上两点,经过点
一上两点,经过点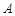 、
、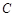 、
、 的抛物线的一部分
的抛物线的一部分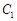 与经过点
与经过点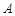 、
、
 的抛物线的一部分
的抛物线的一部分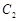 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点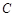 的坐标为
的坐标为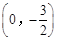 ,点
,点 是抛物线
是抛物线 的顶点.
的顶点.
(1)求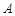 、
、 两点的坐标;
两点的坐标;
(2)“蛋线”在第四象限上是否存在一点 ,使得
,使得 的面积最大?若存在,求出
的面积最大?若存在,求出 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)当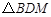 为直角三角形时,求
为直角三角形时,求 的值.
的值.
由于受金融危机的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若乙型号手机的售价为1400元,为了促销,公司决定每售出一台乙型号手机,返还顾客现金a元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同,a应取何值?
如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种
植草坪的概率是多少(用树状图或列表法求解)?
某中学食堂为学生提供了四种价格的午餐供其选择,这四种价格分别是:A:3元,B:4元,C:5元,D:6元.为了解学社对四种午餐的购买情况,学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况,依据统计数据制成如下的统计图表: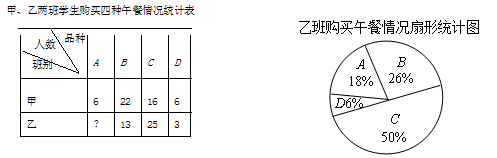
(1)求乙班学生人数;
(2)求乙班购买午餐费用的中位数;
(3)已知甲、乙两班购买午餐费用的平均数均为4.44元,从平均数和众数的角度分析,哪个班购买的餐价格较高;
(4)从这次接受调查的学生中,随机抽查一人,恰好是购买C种午餐的学生的概率是多少?
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.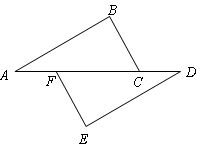
(1)解不等式组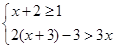
(2)解方程:x2+3x-2=0;