已知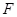 为抛物线
为抛物线 的焦点,抛物线上点
的焦点,抛物线上点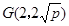 满足
满足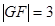
(Ⅰ)求抛物线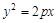 的方程;
的方程;
(Ⅱ)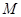 点的坐标为(
点的坐标为(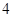 ,
, ),过点F作斜率为
),过点F作斜率为 的直线与抛物线交于
的直线与抛物线交于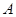 、
、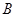 两点,
两点,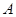 、
、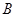 两点的横坐标均不为
两点的横坐标均不为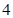 ,连结
,连结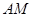 、
、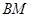 并延长交抛物线于
并延长交抛物线于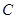 、
、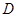 两点,设直线
两点,设直线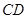 的斜率为
的斜率为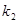 ,问
,问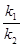 是否为定值,若是求出该定值,若不是说明理由.
是否为定值,若是求出该定值,若不是说明理由.
(本小题满分12分)
已知二次函数 ,且
,且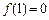 .
.
(1)若函数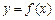 与x轴的两个交点
与x轴的两个交点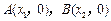 之间的距离为2,求b的值;
之间的距离为2,求b的值;
(2)若关于x的 方程
方程 的两个实数根分别在区间
的两个实数根分别在区间 内,求b的取值范
内,求b的取值范 围.
围.
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(Ⅰ)求箱产品被用户接收的概率;
(Ⅱ)记抽检的产品件数为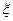 ,求
,求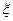 的分布列和数期望.
的分布列和数期望.
在 中,
中,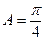 ,
,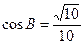 .
.
(Ⅰ)求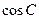 ;
;
(Ⅱ)设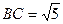 ,求
,求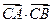 的值.
的值.
已知数列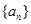 ,
, .
.
(1)求证:数列 为等比数列;
为等比数列;
(2)数列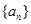 中,是否存在连续的三项,这三项构成等比数列?试说明理由;
中,是否存在连续的三项,这三项构成等比数列?试说明理由;
(3)设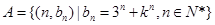 ,其中
,其中 为常数,且
为常数,且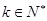 ,
,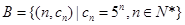 ,求
,求 .
.
已知指数函数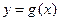 满足:
满足: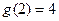 ,定义域为
,定义域为 的函数
的函数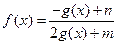
是奇函数。(1)求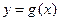 的解析式;
的解析式;
(2)求m,n的值;
(3)若对任意的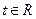 ,不等式
,不等式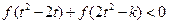 恒成立,求实数
恒成立,求实数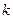 的取值范围。
的取值范围。