为了提高产品的年产量,某企业拟在2013年进行技术改革.经调查测算,产品当年的产量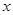 万件与投入技术改革费用
万件与投入技术改革费用 万元(
万元(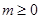 )满足
)满足 (
( 为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的
为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的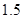 倍(生产成本包括固定投入和再投入两部分资金).
倍(生产成本包括固定投入和再投入两部分资金).
(Ⅰ)试确定的 值,并将2013年该产品的利润
值,并将2013年该产品的利润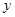 万元表示为技术改革费用
万元表示为技术改革费用 万元的函数(利润=销售金额―生产成本―技术改革费用);
万元的函数(利润=销售金额―生产成本―技术改革费用);
(Ⅱ)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?
已知曲线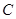 的极坐标方程为
的极坐标方程为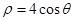 ,以极点为原点,极轴为
,以极点为原点,极轴为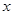 轴的正半轴建立平
轴的正半轴建立平
面直角坐标系,设直线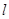 的参数方程为
的参数方程为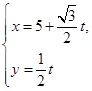 (
(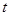 为参数)。
为参数)。
(1)求曲线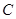 的直角坐标方程与直线
的直角坐标方程与直线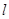 的普通方程;
的普通方程;
(2)设曲线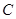 与直线
与直线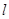 相交于
相交于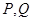 两点,以
两点,以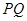 为一条边作曲线
为一条边作曲线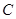 的内接矩形,求该矩形的面积。
的内接矩形,求该矩形的面积。
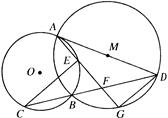
如图,已知 和
和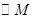 相交于
相交于 两点,
两点,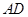 为
为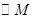 的直径,直线
的直径,直线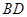 交
交 于点
于点 ,点
,点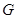 为
为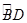 的中点,连接
的中点,连接 分别交
分别交 ,
,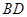 于点
于点 ,连接
,连接 。
。
(1)求证: ;
;
(2)求证: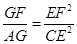 。
。
(本小题满分12分)已知 .
.
(1)已知函数h(x)=g(x)+ax3的一个极值点为1,求 的取值;
的取值;
(2) 求函数 在
在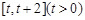 上的最小值;
上的最小值;
(3)对一切 ,
,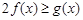 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆右顶点到直线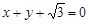 的距离为
的距离为 ,离心率
,离心率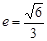
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A为椭圆与y轴负半轴的交点,设直线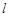 :
: ,是否存在实数m,使直线
,是否存在实数m,使直线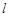 与椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
与椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
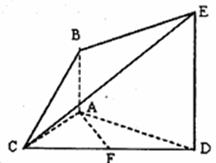
(本小题满分12分)如图,已知 ⊥平面
⊥平面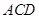 ,
, ,
,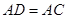
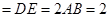 ,且
,且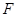 是
是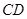 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面 ⊥平面
⊥平面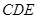 ;
;
(3)求此多面体的体积.