数列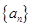 对任意
对任意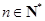 ,满足
,满足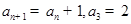 .
.
(1)求数列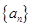 通项公式;
通项公式;
(2)若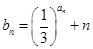 ,求
,求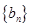 的通项公式及前
的通项公式及前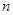 项和.
项和.
(本小题满分15分)已知公差大于零的等差数列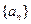 的前n项和为Sn,且满足:
的前n项和为Sn,且满足: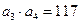 ,
,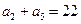 .
.
(1)求数列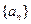 的通项公式
的通项公式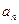 ;
;
(2)若数列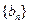 是等差数列,且
是等差数列,且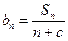 ,求非零常数c.
,求非零常数c.
(本小题满分14分)已知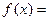
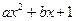 .
.
(1)若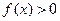 的解集是
的解集是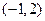 ,求实数
,求实数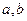 的值.
的值.
(2)若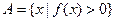 ,且
,且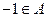 ,
,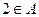 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)在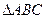 中,已知
中,已知 ,
,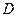 是
是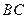 边上的一点,
边上的一点,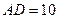 ,
,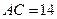 ,
,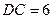 ,求
,求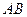 的长.
的长.
(本小题满分10分)
将一枚硬币连续抛掷 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为 ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为 .
.
(Ⅰ)若该硬币均匀,试求 与
与 ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为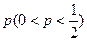 ,试比较
,试比较 与
与 的大小.
的大小.
(本小题满分10分)
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC, ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.