(本小题满分10分)
将一枚硬币连续抛掷 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为 ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为 .
.
(Ⅰ)若该硬币均匀,试求 与
与 ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为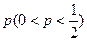 ,试比较
,试比较 与
与 的大小.
的大小.
如图3,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长
为多少时,盒子容积最大?
(图3)
(本题12分)
(1)已知圆的方程是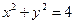 ,求斜率等于1的圆的切线的方程;
,求斜率等于1的圆的切线的方程;
(2)若实数 ,满足
,满足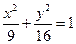 且
且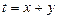 ,求
,求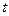 的取值范围;
的取值范围;
(本题12分).已知集合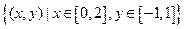
(1)若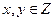 ,求
,求 的概率;
的概率;
(2)若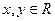 ,求
,求 的概率。
的概率。
(椭圆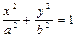
 >
>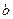 >
>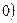 与直线
与直线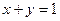 交于
交于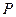 、
、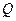 两点,且
两点,且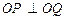 ,其中
,其中 为坐标原点.
为坐标原点.
(1)求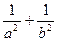 的值;
的值;
(2)若椭圆的离心率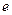 满足
满足 ≤
≤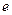 ≤
≤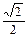 ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
(已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,- )
)
(Ⅰ)求双曲线方程;
(Ⅱ)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(Ⅲ)求△F1MF2的面积.