(已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,- )
)
(Ⅰ)求双曲线方程;
(Ⅱ)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(Ⅲ)求△F1MF2的面积.
(本小题满分13分)设关于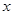 的一元二次方程
的一元二次方程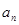
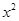

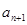
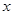
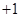
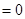 (
(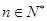 )有两根
)有两根 和
和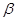 ,且满足
,且满足 .
.
(1)试用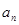 表示
表示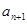 ;
;
(2)求证:数列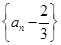 是等比数列;
是等比数列;
(3)当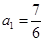 时,求数列
时,求数列 的通项公式,并求数列
的通项公式,并求数列 的前
的前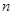 项和
项和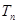 .
.
(本小题满分13分)函数y=Asin(ωx+ )(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=
)(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=
π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin( )>Asin(
)>Asin( )?若存在,求出m值(或范围),若不存在,请说明理由.
)?若存在,求出m值(或范围),若不存在,请说明理由.
(本小题满分12分)在棱长为2的正方体 中,设
中,设 是棱
是棱 的中点.
的中点.
(1)求证: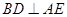 ;
;
(2)求证: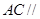 平面
平面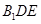 ;
;
(3)求三棱锥 的体积.
的体积.
(本小题满分12分)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段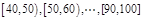 ,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题: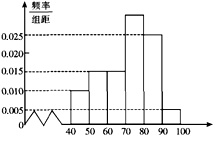
(1)求70~80分数段的学生人数;
(2)估计这次考试中该学科的优分率(80分及以上为优分)、中位数、平均值;
(3)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
(本小题满分12分)已知
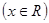 .
.
(Ⅰ)求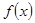 的最小正周期;
的最小正周期;
(Ⅱ)求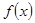 的单调增区间;
的单调增区间;
(Ⅲ)若
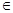 [
[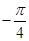 ,
, ]时,求
]时,求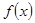 的值域.
的值域.