如图,一台起重机,他的机身高AC为21m,吊杆AB长为36m,吊杆与水平线的夹角∠BAD可从30°升到80°.求这台起重机工作时,吊杆端点B离地面CE的最大高度和离机身AC的最大水平距离(结果精确到0.1m). (参考数据:sin80°≈0.98,cos80°≈0.17,tan33°≈5.67, ≈1.73)
≈1.73)
在如图所示的正方形网格中,点A、B、C在小正方形的顶点上.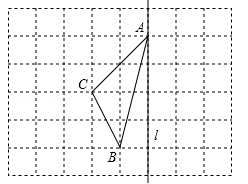
(1)在图中画出与△ABC关于直线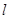 成轴对称的△AB′C′;
成轴对称的△AB′C′;
(2)线段C C′被直线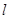 .
.
某居民统计了家里的用水量x(立方米)与应缴水费w(元)之间的关系如下表所示.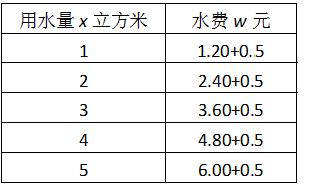
(1)写出用水量x(立方米)与水费w(元)之间的关系式.
(2)计算用水量是35立方米时的水费是多少元?
出租车司机小李某天下午的营运全是在东西走向的人民大街上行驶的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)若小李下午出发地记为0,他将最后一名乘客送抵目的地时距出发地点有多远?
(2)若汽车耗油量为0.41升/ 千米,这天下午小李共耗油多少升?
已知:A-B= ,且B=
,且B=  .
.
(1)求A等于多少?
(2)若 ,求A的值.
,求A的值.
如图是一个数值转换机的示意图.
请观察示意图,理解运算原理,用代数式表示出来.若输入x的值为3,y的值为-2,输出的结果是多少?