某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(1)求第n年初M的价值an的表达式;
(2)求数列 的前n项和
的前n项和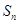
(本小题满分12分)
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)。有甲乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(Ⅰ)求出甲、乙两人所付租车费用相同的概率;
(Ⅱ)设甲、乙两人所付的租车费用之和为随机变量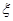 ,求
,求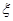 的分布列与数学期望
的分布列与数学期望 ;
;
.
如图甲,直角梯形 中,
中, ,
, ,点
,点 、
、 分别在
分别在 ,
, 上,且
上,且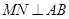 ,
,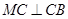 ,
, ,
, ,现将梯形
,现将梯形 沿
沿 折起,使平面
折起,使平面 与平面
与平面 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当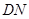 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为 ?
?
已知等差数列 的前
的前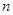 项和为
项和为 ,且
,且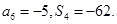
(1)求 通项公式;
通项公式;
(2)求数列 的前
的前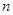 项和
项和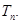
如图,某观测站C在城A的南偏西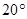 的方向,从城A出发有一条走向为南偏东
的方向,从城A出发有一条走向为南偏东 的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?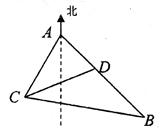
设函数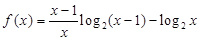
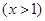 .
.
(I)求函数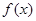 的最小值;
的最小值;
(Ⅱ)若 ,且
,且 ,求证:
,求证: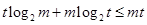 ;
;
(Ⅲ)若 ,且
,且 ,
,
求证: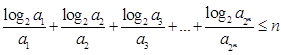 .
.