已知数列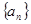 是等差数列,
是等差数列,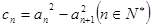
(1)判断数列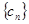 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果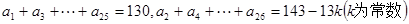 ,试写出数列
,试写出数列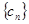 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列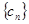 得前n项和为
得前n项和为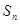 ,问是否存在这样的实数
,问是否存在这样的实数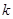 ,使
,使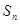 当且仅当
当且仅当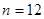 时取得最大值。若存在,求出
时取得最大值。若存在,求出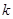 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
方程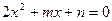 有实根,且2、
有实根,且2、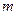 、
、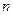 为等差数列的前三项.求该等差数列公差
为等差数列的前三项.求该等差数列公差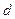 的取值范围.
的取值范围.
已知等差数列前三项为a,4,3a,前n项的和为Sn,Sk=2550.
(Ⅰ)求a及k的值;
(Ⅱ)求
求函数y=(sinx+cosx)2+2cos2x的最小正周期.
已知 ,试用
,试用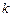 表示
表示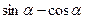 的值.
的值.
已知复数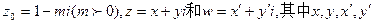 均为实数,
均为实数,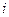 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数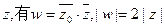 。
。
(1)试求 的值,并分别写出
的值,并分别写出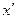 和
和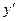 用
用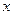 、
、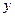 表示的关系式;
表示的关系式;
(2)将(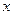 、
、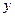 )作为点
)作为点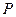 的坐标,(
的坐标,(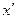 、
、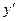 )作为点
)作为点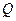 的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点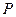 变到这一平面上的点
变到这一平面上的点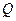 ,
,
当点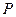 在直线
在直线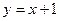 上移动时,试求点
上移动时,试求点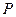 经该变换后得到的点
经该变换后得到的点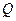 的轨迹方程;
的轨迹方程;
(3)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由。