如图所示制作一种产品，需先将材料加热达到60℃后，再进行操作。设该材料温度为y（℃），从加热开始计算的时间为x（min）。据了解，设该材料开始加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y 与时间x成反比例关系（如图）。已知该材料在操作加工前的温度为20℃，加热5分钟后温度达到60℃。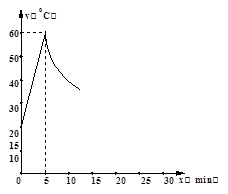
（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式。
（2）根据工艺要求，是材料的温度低于15℃，需停止操作，那么从开始加热到停止操作，共经历了多少时间。
如图所示，在Rt△OAB中，∠OAB=90
，且点B的坐标为（4，2）．画出△OAB绕点O逆时针旋转90后的△
，并求出
的长．
已知
，求
的值．
用适当的方法解方程：
如图，在矩形ABCD中，AD=18cm，AB=7cm，动点P、Q分别同时从A、C出发，点
以3cm／s的速度向D移动，直到D为止，点Q以2cm／s的速度向B移动，点停止时，点
也随之停止．
（1）、两点从出发开始几秒时，四边形PQCD的面积是矩形面积的
？
（2）、从开始出发几秒时，
cm?
如图，抛物线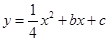
的顶点为M，对称轴是直线x＝1，与x轴的交点为A（－3，0）和B．将抛物线
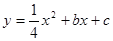绕点B逆时针方向旋转90°，点M1，A1为点M，A旋转后的对应点，旋转后的抛物线与y轴相交于C，D两点．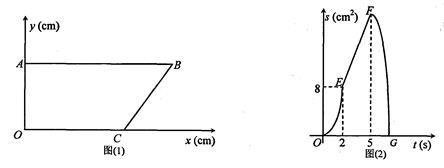
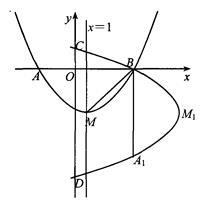
（1）写出点B的坐标及求抛物线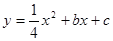的解析式：
（2）求证：∠AMA1=180°
（3）设点P是旋转后抛物线上DM1之间的一动点，是否存在一点P，使四边形PM1MD的面积最大．如果存在，请求出点P的坐标及四边形PM1MD的最大面积；如果不存在，请说明理由．