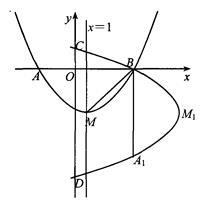
如图，抛物线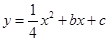
的顶点为M，对称轴是直线x＝1，与x轴的交点为A（－3，0）和B．将抛物线
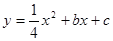绕点B逆时针方向旋转90°，点M1，A1为点M，A旋转后的对应点，旋转后的抛物线与y轴相交于C，D两点．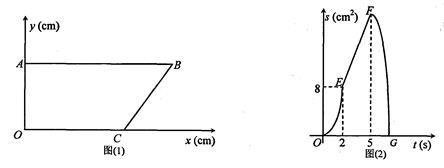
（1）写出点B的坐标及求抛物线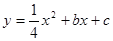的解析式：
（2）求证：∠AMA1=180°
（3）设点P是旋转后抛物线上DM1之间的一动点，是否存在一点P，使四边形PM1MD的面积最大．如果存在，请求出点P的坐标及四边形PM1MD的最大面积；如果不存在，请说明理由．
扬州市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售。求平均每次下调的百分率。
某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米98元，试问哪种方案更优惠？
甲、乙、丙、丁四位同学进行一次羽毛球单打比赛，要从中选出两位同学打第一场比赛．请用树状图法或列表法，求恰好选中甲、乙两位同学的概率；
若已确定甲打第一场，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率。
学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计.图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:求该班共有多少名学生?
在图(1)中,将表示“步行”的部分补充完整.
在扇形统计图中，计算出“骑车”部分所对应的圆心角的度数.
如果全年级共500名同学,请你估算全年级步行上学的学生人数.
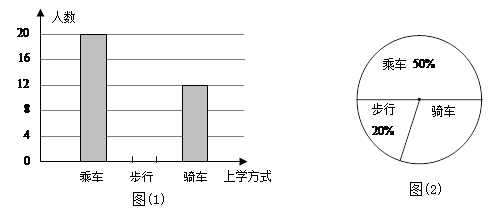
先化简
，然后从
，1，－1中选取一个你认为合适的数作为x的值代入求值．
如图1，在矩形ABCD中，AB＝8，AD＝6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP＝CQ．设AP＝x．当PQ∥AD时， x的值等于；
如图2，线段PQ的垂直平分线EF与BC边相交于点E，连接EP、EQ，设BE= y，求y关于x的函数关系式；
在问题（2）中，设△EPQ的面积为S，求S关于x的函数关系式，并求当x取何值时，S的值最小，最小值是多少？
