已知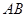 是半圆
是半圆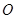 的直径, 点
的直径, 点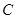 在
在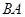 的延长线上运动(点
的延长线上运动(点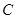 与点
与点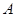 不重合), 以
不重合), 以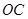 为直径的半圆
为直径的半圆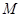 与半圆
与半圆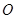 交于点
交于点 的平分线与半圆
的平分线与半圆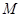 交于点
交于点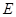 .
.
如图甲, 求证: 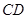 是半圆
是半圆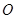 的切线;
的切线;
如图乙, 作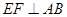 于点
于点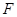 , 猜想
, 猜想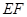 与已有的哪条线段的一半相等, 并加以证明;
与已有的哪条线段的一半相等, 并加以证明;
如图丙, 在上述条件下, 过点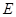 作
作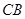 的平行线交
的平行线交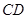 于点
于点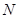 , 当
, 当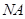 与半圆
与半圆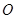 相切时, 求
相切时, 求
甲 乙 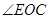 的正切值.
的正切值.
已知关于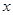 的方程
的方程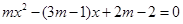
(1)求证:无论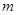 取任何实数时,方程恒有实数根;
取任何实数时,方程恒有实数根;
(2)若关于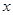 的二次函数
的二次函数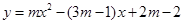 的图象与
的图象与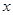 轴两交点间的距离为2时,求抛物线的解析式.
轴两交点间的距离为2时,求抛物线的解析式.
如图,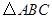 是等腰三角形,
是等腰三角形,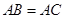 ,以
,以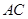 为直径的
为直径的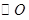 与
与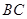 交于点
交于点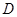 ,
,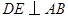 ,垂足为
,垂足为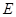 ,
,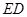 的延长线与
的延长线与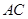 的延长线交于点
的延长线交于点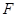 .
.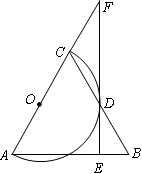
(1)求证: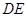 是
是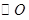 的切线;
的切线;
(2)若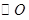 的半径为2,
的半径为2,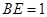 ,求
,求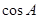 的值.
的值.
在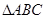 中,
中,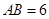 cm ,
cm ,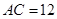 cm ,动点
cm ,动点 以1cm/s 的速度从点
以1cm/s 的速度从点 出发到点
出发到点 止,动点
止,动点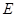 以2cm/s 的速度从点
以2cm/s 的速度从点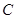 出发到点
出发到点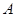 止,且两点同时运动,当以点
止,且两点同时运动,当以点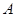 、
、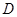 、
、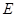 为顶点的三角形与
为顶点的三角形与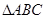 相似时,求运动的时间.
相似时,求运动的时间.
如图,⊙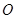 中,弦
中,弦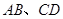 相交于
相交于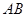 的中点
的中点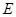 ,连接
,连接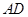 并延长至点
并延长至点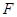 ,
,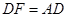 ,连接BC、
,连接BC、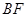 .
.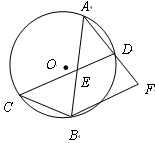
(1)求证: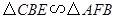 ;
;
(2)当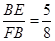 时,求
时,求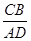 的值.
的值.
某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件.经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.将销售价定为多少时,才能使每天所获销售利润最大?最大利润是多少?