如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中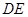 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,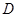 在
在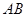 上,
上,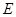 在
在 上.
上.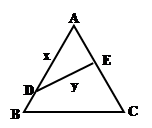
(1)设 ,求用
,求用 表示
表示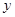 的函数关系式;
的函数关系式;
(2)如果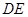 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,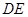 的位置应在哪里?如果
的位置应在哪里?如果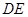 是参观线路,则希望它最长,
是参观线路,则希望它最长,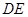 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
已知点 是离心率为
是离心率为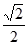 的椭圆
的椭圆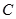 :
: 上的一点,斜率为
上的一点,斜率为 的直线
的直线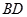 交椭圆
交椭圆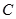 于
于 、
、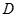 两点,且
两点,且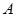 、
、 、
、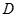 三点不重合.
三点不重合.
(1)求椭圆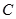 的方程;
的方程;
(2)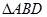 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
已知四棱锥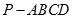 的底面是菱形.
的底面是菱形.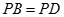 ,
,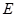 为
为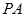 的中点.
的中点.
(1)求证: ∥平面
∥平面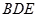 ;
;
(2)求证:平面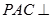 平面
平面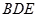 .
.
已知等差数列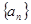 满足
满足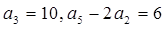 .
.
(Ⅰ)求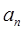 ;
;
(Ⅱ)数列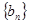 满足
满足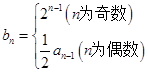 ,
, 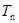 为数列
为数列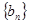 的前
的前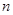 项和,求
项和,求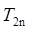 .
.
各项均为正数的等差数列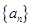 首项为1,且
首项为1,且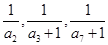 成等比数列,
成等比数列,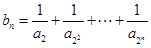
(1)求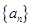 、
、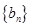 通项公式;
通项公式;
(2)求数列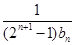 前n项和
前n项和 ;
;
(3)若对任意正整数n都有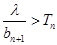 成立,求
成立,求 范围.
范围.
已知椭圆E: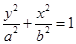 (
(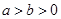 )离心率为
)离心率为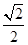 ,上顶点M,右顶点N,直线MN与圆
,上顶点M,右顶点N,直线MN与圆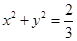 相切,斜率为k的直线l经过椭圆E在正半轴的焦点F,且交E于A、B不同两点.
相切,斜率为k的直线l经过椭圆E在正半轴的焦点F,且交E于A、B不同两点.
(1)求E的方程;
(2)若点G(m,0)且| GA|=| GB|, ,求m的取值范围.
,求m的取值范围.