某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)若该校高一年级共有学生 人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(2)若从数学成绩在 与
与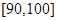 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。
【2015高考浙江,理18】已知函数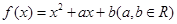 ,记
,记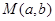 是
是 在区间
在区间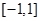 上的最大值.
上的最大值.
(1)证明:当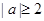 时,
时,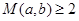 ;
;
(2)当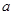 ,
,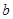 满足
满足 ,求
,求 的最大值.
的最大值.
如图,已知椭圆 与
与 的中心在坐标原点
的中心在坐标原点 ,长轴均为
,长轴均为 且在
且在 轴上,短轴长分别为
轴上,短轴长分别为 ,
,
 ,过原点且不与
,过原点且不与 轴重合的直线
轴重合的直线 与
与 ,
, 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为 、
、 、
、 、
、 .记
.记 ,
, 和
和 的面积分别为
的面积分别为 和
和 .
.
(1)当直线 与
与 轴重合时,若
轴重合时,若 ,求
,求 的值;;
的值;;
(2)设直线 ,若
,若 ,证明:
,证明: 是线段
是线段 的四等分点
的四等分点
(3)当 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线 ,使得
,使得 ?并说明理由.
?并说明理由.
对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意的
对于任意的 都成立,我们称这个数列
都成立,我们称这个数列 是“
是“ 类数列”.
类数列”.
(1)若 ,判断数列
,判断数列 是否为“
是否为“ 类数列”,并说明理由;
类数列”,并说明理由;
(2)若数列 是“
是“ 类数列”,则数列
类数列”,则数列 、
、 是否一定是“
是否一定是“ 类数列”,若是的,加以证明;若不是,说明理由;
类数列”,若是的,加以证明;若不是,说明理由;
(3)若数列 满足:
满足: ,设数列
,设数列 的前
的前 项和为
项和为 ,求
,求 的表达式,并判断
的表达式,并判断 是否是“
是否是“ 类数列”.
类数列”.
如图,某污水处理厂要在一个矩形 的池底水平铺设污水净化管道(直角
的池底水平铺设污水净化管道(直角 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是 的中点,
的中点, 分别落在
分别落在
 上,且
上,且 ,设
,设 .
.
(1)试将污水管道的长度 表示成
表示成 的函数,并写出定义域;
的函数,并写出定义域;
(2)当管道长度 为何值时,污水净化效果最好,并求此时管道的长度.
为何值时,污水净化效果最好,并求此时管道的长度.
如图,已知正四棱柱 中,底面边长
中,底面边长 ,侧棱
,侧棱 的长为4,过点
的长为4,过点 作
作 的垂线交侧棱
的垂线交侧棱 于点
于点 ,交
,交 于点
于点 .
.
(1)求证: ⊥平面
⊥平面 ;
;
(2)求三棱锥 的体积.
的体积.