如图,在几何体
中,四边形
是矩形,
平面
,
,
,
分别是线段
的中点.
(Ⅰ)求证:
平面
;
(Ⅱ)求平面
与平面
所成锐二面角的余弦值.
某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定.
(Ⅰ)求当天小王的该银行卡被锁定的概率;
(Ⅱ)设当天小王用该银行卡尝试密码次数为
,求
的分布列和数学期望.
已知椭圆 ,过点 且不过点 的直线与椭圆 交于
两点,直线
与直线
交于点
.
(Ⅰ)求椭圆
的离心率;
(Ⅱ)若
垂直于
轴,求直线
的斜率;
(Ⅲ)试判断直线
与直线
的位置关系,并说明理由.
设函数
,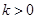 .
.
(Ⅰ)求
的单调区间和极值;
(Ⅱ)证明:若
存在零点,则
在区间
上仅有一个零点.
如图,在三棱锥 中,平面 平面 , 为等边三角形, 且 . 分别为 , 的中点.

(Ⅰ)求证:
平面
;
(Ⅱ)求证:平面
平面
;
(Ⅲ)求三棱锥
的体积.