某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
现有三张不透明的卡片,其中两张卡片的正面图案为"神舟首飞",第三张卡片的正面图案为"保卫和平",卡片除正面图案不同外,其余均相同.将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求两次抽出的卡片上的图案都是"保卫和平"的概率.(图案为"神舟首飞"的两张卡片分别记为 、 ,图案为"保卫和平"的卡片记为

先化简,再求值: ,其中 .
如图,已知点 、 , ,点 为线段 上的一个动点,反比例函数 的图象经过点 .小明说:"点 从点 运动至点 的过程中, 值逐渐增大,当点 在点 位置时 值最小,在点 位置时 值最大."
(1)当 时.
①求线段 所在直线的函数表达式.
②你完全同意小明的说法吗?若完全同意,请说明理由;若不完全同意,也请说明理由,并求出正确的 的最小值和最大值.
(2)若小明的说法完全正确,求 的取值范围.

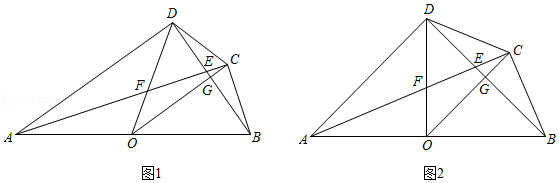
如图1,已知点 在四边形 的边 上,且 , 平分 ,与 交于点 , 分别与 、 交于点 、 .
(1)求证: ;
(2)如图2,若 ,求 的值;
(3)当四边形 的周长取最大值时,求 的值.
阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数 、 满足 ①, ②,求 和 的值.
本题常规思路是将①②两式联立组成方程组,解得 、 的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由① ②可得 ,由① ② 可得 .这样的解题思想就是通常所说的"整体思想".
解决问题:
(1)已知二元一次方程组 则 , ;
(2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?
(3)对于实数 、 ,定义新运算: ,其中 、 、 是常数,等式右边是通常的加法和乘法运算.已知 , ,那么 .