2013年，首都北京经历了59年来雾霾天气最多的一个月。经气象局统计，北京市从1月1日至1月30日这30天里有26天出现雾霾天气。《环境空气质量指数（AQI）技术规定（试行）》将空气质量指数分为六级：其中，中度污染（四级），指数为151—200；重度污染（五级），指数为201—300；严重污染（六级），指数大于300． 下面表1是该观测点记录的4天里，AQI指数
与当天的空气水平可见度
（千米）的情况，表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果，
表1：AQI指数与当天的空气水平可见度（千米）情况
| AQI指数 |
 |
 |
 |
 |
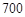| 空气可见度（千米） |
 |
 |
 |
 |
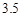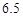表2：北京1月1日到1月30日AQI指数频数统计
| AQI指数 |
 |
 |
 |
 |
 |
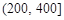| 频数 |
3 |
6 |
12 |
6 |
3 |
（Ⅰ）设变量
，根据表1的数据，求出关于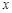
的线性回归方程；
（Ⅱ）根据表2估计这30天AQI指数的平均值.
（用最小二乘法求线性回归方程系数公式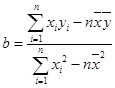
，
）
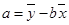