某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
| 时间x(天) |
0 |
4 |
8 |
12 |
16 |
20 |
| 销量y1(万朵) |
0 |
16 |
24 |
24 |
16 |
0 |
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如下图所示.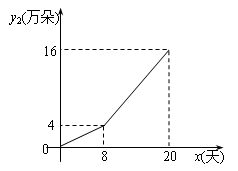
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;
(2)观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;
(3)设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.
“五一”节,小莉和同学一起到游乐场玩,游乐场的大型摩天轮的半径为20m,匀速旋转1周需要12min.小莉乘坐最底部的车厢(离地面0. 5m)开始1周的观光,5min后小莉离地面的高度是多少?
(精确到0.1m,下列数据供参考: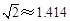 ;
;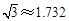 ;
;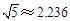 )
)

如图,正方形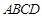 的边长为12,其内部有一个小正方形
的边长为12,其内部有一个小正方形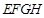 ,其中
,其中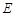 、
、 、
、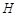 分别在
分别在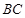
 、
、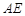 上.若
上.若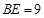 ,求小正方形
,求小正方形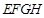 的边长.
的边长.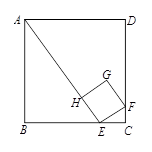
排球比赛规定每局需决出胜负.水平相当的甲、乙两队进行排球比赛,规定五局三胜,求甲队以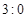 战胜乙队的概率.
战胜乙队的概率.
甲、乙两篮球运动员上赛季每场比赛的得分如下:
甲15,24,25,31,31,36,36,37,39,44,50.
乙8,13,14,16,23,26,28,33,38,39,51.
小莉用如图的方式来表示甲、乙的得分.
(1)请在右侧补全乙的得分;
(2)用不等号填空: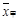
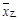 ;
;
 ;
;
(3)请说出此种表示方式的优点.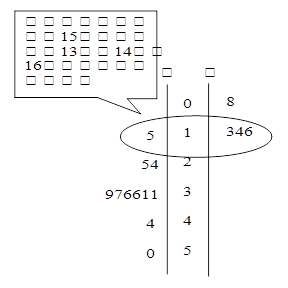
妈妈给小莉100元去超市购买笔记本,已知笔记本每本12元.
请你根据以上信息,提出一个用一元一次不等式解决的问题,并写出解答过程.