在一个布口袋里装着白、红、黑三种颜色的小球，它们除颜色之外没有任何其它区别，其中有白球3只、红球2只、黑球1只．袋中的球已经搅匀．
（1）闭上眼睛随机地从袋中取出1只球，求取出的球是黑球的概率；
（2）若取出的第1只球是红球，将它放在桌上，闭上眼睛从袋中余下的球中再随机地取出1只球，这时取出的球还是红球的概率是多少？
（3）若取出一只球，将它放回袋中，闭上眼睛从袋中再随机地取出1只球，两次取出的球都是白球概率是多少？（用列表法或树状图法计算）
有一张长9cm，宽3cm的矩形纸片，如图所示，把它折叠使D点与B点重合，你能求出DE,EF的长吗？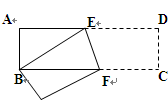
铁路上A， B两站（两站间视为直线），相距25km，C，D为两村庄（视为两个点），DA⊥AB于A,CB⊥AB于B（如图），已知DA="15km,CB=10km," 现在要在铁路AB上建设一个土特产品收购站E，使得C,D两村庄到E站距离相等，则E站应建在距离A站多远处？ 
如图，
是△
的外角
的平分线，交
的延长线于
，延长
交△的外接圆于点
，连结
，
．
（1）求证：
；
（2）求证：
；
（3）若
是△外接圆的直径，
，
，求的长．
如图，已知
是
外任意一点，过点作直线
，
，分别交于点
，
，
，
．求证：
（
的度数
的度数）．
如图，
为
的直径，
，垂足为
，
，
与
交于
．
（1）求证：
；
（2）若
，
把半圆三等分，
，求
的长．