已知数列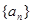 ,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,
,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,
(1)令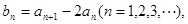 证明
证明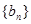 是等比数列,并求
是等比数列,并求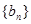 的通项公式;
的通项公式;
(2)令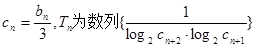 的前n项和,求
的前n项和,求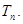
若 、
、 为双曲线
为双曲线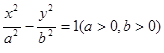 的左右焦点,O为坐标原点,P在双曲线左支,
的左右焦点,O为坐标原点,P在双曲线左支, 在右准线上,且满足
在右准线上,且满足 ,
,
(1)求双曲线离心率;
(2)若双曲线过点N(2, ),它的虚轴端点为
),它的虚轴端点为 ,
,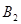 (
( 在
在 轴正半轴上)过
轴正半轴上)过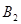 作直线
作直线 与双曲线交于A、B两点,当
与双曲线交于A、B两点,当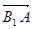 ⊥
⊥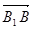 时,求直线
时,求直线 的方程。
的方程。
长度为 的线段AB的两个端点A、B在抛物线
的线段AB的两个端点A、B在抛物线 上运动,求AB中点到
上运动,求AB中点到 轴的最短距离。
轴的最短距离。
如图,在直四棱柱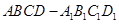 中,底面
中,底面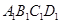 是梯形,且
是梯形,且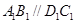 ,
,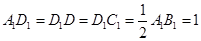 ,
,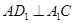 ,
,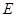 是棱
是棱 的中点.
的中点.
(1)求证: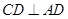 ;
;
(2)求点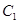 到平面
到平面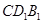 的距离;
的距离;
(3)求二面角 的大小.
的大小.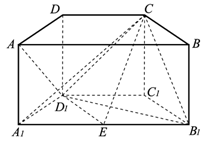
在五棱锥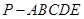 中,
中,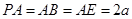 ,
,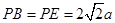 ,
,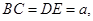

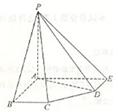
(1)求证: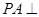 平面
平面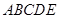 ;
;
(2)求二面角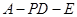 的大小;
的大小;
(3)求点C到平面PDE的距离.