已知向量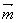 =(
=(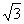 sin2x+2,cosx),
sin2x+2,cosx),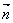 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 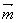 ·
·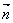 .
.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若a=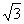 ,f(A)=4,求b+c的最大值.
,f(A)=4,求b+c的最大值.
用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台。
如图,在四棱台 中,下底
中,下底 是边长为
是边长为 的正方形,上底
的正方形,上底 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 ⊥平面
⊥平面 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求平面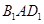 与平面
与平面 夹角的余弦值.
夹角的余弦值.
如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
已知在等比数列 中,
中, ,且
,且 是
是 和
和 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)若数列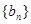 满足
满足 ,求
,求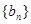 的前
的前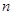 项和
项和 .
.
已知向量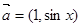 ,
, ,函数
,函数
(1)求函数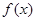 的解析式及其单调递增区间;
的解析式及其单调递增区间;
(2)在 中,角
中,角 为钝角,若
为钝角,若 ,
, ,
,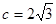 .求
.求 的面积。
的面积。
若双曲线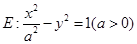 的离心率等于
的离心率等于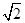 ,直线
,直线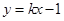 与双曲线
与双曲线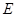 的右支交于
的右支交于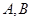 两点.
两点.
(1)求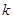 的取值范围;
的取值范围;
(2)若 ,点
,点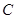 是双曲线
是双曲线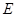 上一点,且
上一点,且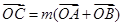 ,求
,求