若双曲线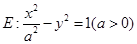 的离心率等于
的离心率等于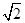 ,直线
,直线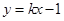 与双曲线
与双曲线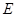 的右支交于
的右支交于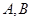 两点.
两点.
(1)求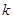 的取值范围;
的取值范围;
(2)若 ,点
,点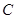 是双曲线
是双曲线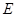 上一点,且
上一点,且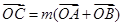 ,求
,求
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
求点A到平面A1DE的距离;
求证:CF∥平面A1DE,
求二面角E-A1D-A的平面角大小的余弦值.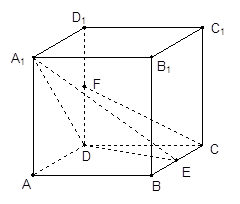
某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人).
(1)共有多少种安排方法?
(2)其中甲、乙两人都被安排的概率是多少?
(3)甲、乙两人中至少有一人被安排的概率是多少?
已知函数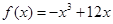 ,①求函数的单调区间;②求函数的极值,③当
,①求函数的单调区间;②求函数的极值,③当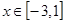 时,求函数的最大值与最小值.
时,求函数的最大值与最小值.
已知复数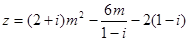 ,当实数
,当实数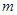 取什么值时,复数
取什么值时,复数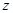 是:
是:
(1)零;
(2)虚数;
(3)纯虚数.
已知椭圆 :
: (
( ),直线
),直线 为圆
为圆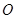 :
: 的一条切线并且过椭圆的右焦点,记椭圆的离心率为
的一条切线并且过椭圆的右焦点,记椭圆的离心率为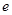 .
.
(1)求椭圆的离心率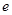 的取值范围;
的取值范围;
(2)若直线 的倾斜角为
的倾斜角为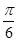 ,求
,求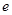 的大小;
的大小;
(3)是否存在这样的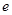 ,使得原点
,使得原点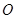 关于直线
关于直线 的对称点恰好在椭圆
的对称点恰好在椭圆 上.若存在,求出
上.若存在,求出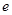 的大小;若不存在,请说明理由.
的大小;若不存在,请说明理由.