（满分13分）学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏，学习雷锋精神时全修好；单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计，具体数据如下：
| |
损坏餐椅数 |
未损坏餐椅数 |
总 计 |
| 学习雷锋精神前 |
50 |
150 |
200 |
| 学习雷锋精神后 |
30 |
170 |
200 |
| 总 计 |
80 |
320 |
400 |
（Ⅰ）求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关？
（Ⅱ）请说明是否有97．5%以上的把握认为损毁餐椅数量与学习雷锋精神有关？
参考公式：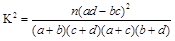
，
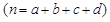
| P（K2≥k0） |
0．05 |
0．025 |
0．010 |
0．005 |
0．001 |
| k0 |
3．841 |
5．024 |
6．635 |
7．879 |
10．828 |
(本小题满分10分)已知等差数列{an}的首项a1＝1，公差d＞0，且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设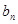
＝
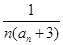（n∈N*），
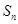＝b1＋b2＋…＋bn，是否存在最大的整数t，使得任意的n均有
总成立？若存在，求出t；若不存在，请说明理由
(本小题满分10分)已知A、B、C为△ABC的三内角，且其对边分别为a、b、c.若
, 
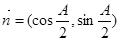，且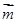
·
＝
.
（1） 求角A的大小； ⑵ 若a＝2
，三角形面积S＝，求b+c的值.
（本小题14分）已知四棱锥P-ABCD，底面ABCD是
、边长为
的菱形，又
，且PD=CD，点M、N分别是棱AD、PC的中点．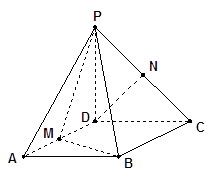
（1）证明：DN//平面PMB；
（2）证明：平面PMB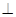
平面PAD；
（3）求点A到平面PMB的距离．
（本小题满分10分）如图，在三棱柱
—
中，点D是BC的中点，欲过点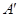
作一截面与平面
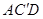平行，问应当怎样画线，并说明理由。
（本小题10分）如图，圆锥形封闭容器，高为h，圆锥内水面高为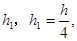
若将圆锥倒置后，圆锥内水面高为
