某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交 元(1≤a≤3)的管理费,预计当每件商品的售价为
元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.
元(8≤x≤9)时,一年的销售量为(10-x)2万件.
(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);
(2)当每件商品的售价为多少元时,该连锁分店一年的利润L最大,并求出L的最
大值M(a).
(本小题满分12分)
已知正方形 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
.
(Ⅰ)试写出正方形另外三个顶点的坐标,并求 ,
, 的值;
的值;
(II)求函数的单调增区间.
(本小题满分12分)
解关于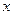 的不等式
的不等式 ,其中
,其中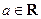 ,且
,且 .
.
(本小题满分14分)
已知函数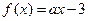 ,
,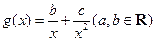 ,且
,且 .
.
(1)试求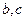 所满足的关系式;
所满足的关系式;
(2)若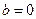 ,方程
,方程 有唯一解,求
有唯一解,求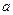 的取值范围.
的取值范围.
已知定义域为 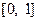 的函数同时满足以下三个条件:
的函数同时满足以下三个条件:
①对任意 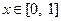 ,总有
,总有 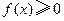 ;
;
② 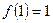 ;
;
③若 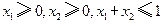 ,则有
,则有 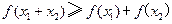 成立.
成立.
(I)求 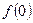 的值;
的值;
(II)判断函数 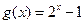 在区间
在区间 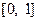 上是否同时适合①②③,并给出证明.
上是否同时适合①②③,并给出证明.
(本小题满分12分)
已知函数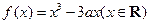 .
.
(Ⅰ)当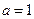 时,求
时,求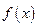 的极小值;
的极小值;
(Ⅱ)若直线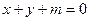 对任意的
对任意的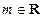 都不是曲线
都不是曲线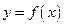 的切线,求
的切线,求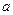 的取值范围.
的取值范围.