已知函数f (x) = 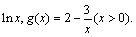
(1)试判断当 的大小关系;
的大小关系;
(2)试判断曲线 和
和 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
(3)试比较 (1 + 1×2) (1 + 2×3) ……(1 +2012×2013)与 的大小,并写出判断过程.
的大小,并写出判断过程.
对于定义域为 的函数
的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在
在 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间 ,使
,使 在
在 上的值域为
上的值域为 ;那么把
;那么把 (
( )叫闭函数,且条件②中的区间
)叫闭函数,且条件②中的区间 为
为 的一个“好区间”.
的一个“好区间”.
(1)求闭函数 的“好区间”;
的“好区间”;
(2)若 为闭函数
为闭函数 的“好区间”,求
的“好区间”,求 、
、 的值;
的值;
(3)判断函数 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数 的取值范围.
的取值范围.
已知函数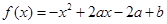 ,且
,且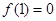 .
.
(1)若 在区间
在区间 上有零点,求实数
上有零点,求实数 的取值范围;
的取值范围;
(2)若 在
在 上的最大值是2,求实数
上的最大值是2,求实数 的的值.
的的值.
已知函数 ,
, .
.
(1)当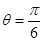 时,求
时,求 的最大值和最小值;
的最大值和最小值;
(2)若 在
在 上是单调函数,且
上是单调函数,且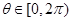 ,求
,求 的取值范围.
的取值范围.
已知 中,点
中,点 在线段
在线段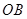 上,且
上,且 ,延长
,延长 到
到 ,使
,使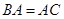 .设
.设 .
.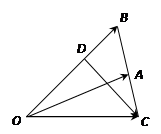
(1)用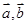 表示向量
表示向量 ;
;
(2)若向量 与
与 共线,求
共线,求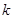 的值.
的值.
已知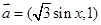 ,
,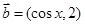 .
.
(1)若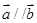 ,求
,求 的值;
的值;
(2)若 ,求
,求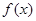 的单调递增区间.
的单调递增区间.