抛物线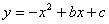
与x轴交与
，
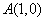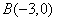两点，
（1）求该抛物线的解析式；
（2）设（1）中的抛物线与y轴交于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．
如图所示,一次函数y=ax+b（a≠0）的图象与反比例函数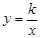
（k≠0）的图象交于M、N两点.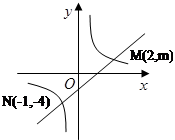
（1）求反比例函数与一次函数的解析式
（2）根据图象写出使反比例函数的值大于一次函数的值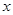
的取值范围.
如图，在□ABCD中，点E、F在BD上，且BF＝DE.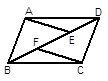
（1）写出图中所有你认为全等的三角形；
（2）请选择一对证明.
如图，某公园入口处原有三级台阶，每级台阶高为20 cm,，深为30 cm，为方便残疾人士，拟将台阶改成斜坡，高台阶的起点为A，斜坡的起始点为C（如图所示），现将斜坡的坡角∠BCA设计为12°，那么斜坡起点C应离A点多远？（精确到1 cm，sin12°=0.208，cos12°=0.978，tan12°=0.213）
小明和小亮是上海某高校的大学生，他们参加世博志愿者选拔并与甲、乙二人都进入了前4名．现从这4名入选者中确定2名作为志愿者．试用画树形图或列表的方法求出小明和小亮同时入选的概率．
在右图中以点p为位似中心，画一个三角形，与原三角形位似，使它与原三角形的位似比是1：2.
