在直角坐标系 内,直线
内,直线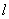 的参数方程为
的参数方程为
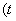 为参数
为参数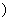 .以
.以 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为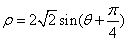 .判断直线
.判断直线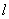 和圆
和圆 的位置关系.
的位置关系.
(本小题满分14分)如图,四棱柱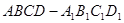 中,
中,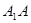 ^底面ABCD,且
^底面ABCD,且 . 梯形ABCD的面积为6,且AD//BC,AD=2BC,AB="2." 平面
. 梯形ABCD的面积为6,且AD//BC,AD=2BC,AB="2." 平面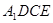 与
与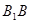 交于点E.
交于点E. 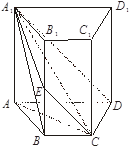
(1)证明:EC//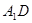 ;
;
(2)求点C到平面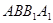 的距离.
的距离.
(本小题满分14分)某家电生产企业根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表:
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工时 |
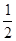 |
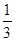 |
 |
| 产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
(本小题满分14分)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
| 时间x |
1 |
2 |
3 |
4 |
5 |
| 命中率y |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
(1)求小李这5天的平均投篮命中率;
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
(本小题满分12分)如图,已知PA^⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC=PA,E是PC的中点,F是PB的中点.
(1)求证:EF//平面ABC;
(2)求证:EF^平面PAC;
(3)求三棱锥B—PAC的体积.
(本小题满分12分)某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示. 质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
| 车间 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.