在真空中速度为v=6.4×107m/s的电子束连续射入两平行板间，如图所示，极板长度L=8.0×10-2m间距d=5.0×10-2m，两极板不带电时，电子将沿极板间的中线通过，在极板上加一个50Hz的交变电压u=U0sinωt，如果所加电压的最大值U0超过某值UC时，电子束将有时能通过两极板，有时间断而不能通过（电子电荷量e=1.6×10-19C，电子质量m=9.1×10-31kg）.求：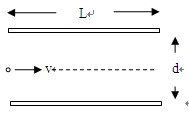
（1）UC的大小为多少；
（2）求U0为何值时，才能使通过与间断的时间之比Δt1∶Δt2=2∶1.
如图所示，A、B两滑环分别套在间距为1m的光滑细杆上，A和B的质量分别为1kg、3kg，用一自然长度为1m的轻弹簧将两环相连，在A环上作用一沿杆方向的、大小为20N的拉力F，当两环都沿杆以相同的加速度运动时，弹簧与杆夹角为53O（cos530=0.6）。求：
（1）弹簧的劲度系数k为多少？
（2）若突然撤去拉力F，在撤去拉力F的瞬间，A的加速度为多大？方向如何？
如图甲所示，在一水平放置的隔板MN的上方，存在一磁感应强度大小为B的匀强磁场，磁场方向如图所示。O为隔板上的一个小孔，通过O点可以从不同方向向磁场区域发射电量为+q，质量为m，速率为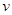
的粒子，且所有入射的粒子都在垂直于磁场的同一平面内运动。不计重力及粒子间的相互作用。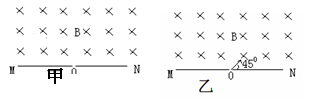
（1）如图乙所示，与隔板成450角的粒子，经过多少时间后再次打到隔板上？此粒子打到隔板的位置与小孔的距离为多少？
（2）所有从O点射入的带电粒子在磁场中可能经过区域的面积为多少？
如图5-14所示，有两个物体A，B，紧靠着放在光滑水平桌面上，A的质量为2kg，B的质量为3kg。有一颗质量为100g的子弹以800m/s的水平速度射入A，经过0.01s又射入物体B，最后停在B中，A对子弹的阻力为3×103N，求A，B最终的速度。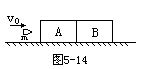
A、B两列火车在同一轨道上同向行驶, A在前, 速度为vA=10m/s, B车在后速度 vB=30m/s. 因大雾能见度低, B车在距A车500m时, 才发现前方有A车. 这时B车立即刹车, 但要经过1800m B车才能停止. 问： A车若仍按原速前进, 两车是否会相撞? （写出具体过程）
如图所示，水平绝缘轨道
与处于竖直平面内的半圆形绝缘光滑轨道
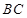平滑连接，半圆形轨道的半径
。轨道所在空间存在水平向右的匀强电场，电场强度
。现有一电荷量
，质量
的带电体(可视为质点)，在水平轨道上的
点由静止释放，已知点与圆形轨道最低点
距离
.带电体与水平轨道间的动摩擦因数
,重力加速度
，取
.求：
(1)带电体运动到圆形轨道的最高点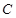
时，速度的大小？
(2)带电体第一次经过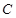点后，落在水平轨道上的位置到点的距离？
(3)带电体在轨道上运动对轨道能产生的最大压力大小？