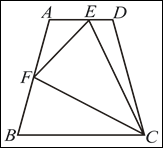
如图，梯形ABCD中，AD∥BC，AB = BC = DC，点E、F分别在AD、AB上，且
.
(1)求证：
；
(2)连结AC，若
，求
的度数.
已知：如图，AC∥DF，直线AF分别直线BD、CE 相交于点G、H，∠1=∠2，求证：∠C=∠D．
某城市对教师试卷讲评课中学生参与的深度与广度进行评价，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制了如下两幅不完整的统计图（图1，图2），请根据图中所给信息解答下列问题：
（1）在这次评价中，一共抽查了名学生；
（2）请将条形图补充完整；
（3）在扇形统计图中，“主动质疑”所对应的扇形圆心角度数为；
（4）如果全市有16万名初中学生，那么在试卷评讲课中，“独立思考”的学生约有多少万人？
如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标。
（2）求出S△ABC
（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A′B′C′，在图中画出△A′B′C′，并写出A′、B′、C′的坐标。
如图，在平面直角坐标系中，抛物线
（
）与x轴相交于A，B两点，与y轴相交于点C，直线
（
）经过B，C两点，已知A（1，0），C（0，3），且BC=5．
（1）分别求直线BC和抛物线的解析式（关系式）；
（2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
如图，在矩形ABCD中，AB=4，AD=6，M，N分别是AB，CD的中点，P是AD上的点，且∠PNB=3∠CBN．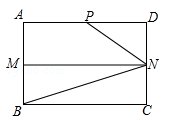
（1）求证：∠PNM=2∠CBN；
（2）求线段AP的长．