一个口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试用概率说明理由.
某厂生产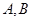 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套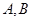 型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套
型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套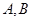 型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产
型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产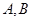 两型会议桌多少套,才能获得最大利润?最大利润是多少?
两型会议桌多少套,才能获得最大利润?最大利润是多少?
已知数列 的前
的前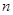 项和
项和 。(1)求数列
。(1)求数列 的通项公式;(2)设
的通项公式;(2)设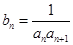 ,且数列
,且数列 的前
的前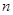 项和为
项和为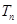 。若
。若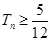 ,求
,求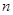 的最小值。
的最小值。
等比数列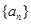 中,已知
中,已知 。(1)求数列
。(1)求数列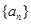 的通项公式;(2)已知数列
的通项公式;(2)已知数列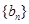 是等差数列,且
是等差数列,且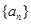 和
和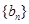 的第2项、第4项分别相等。若数列
的第2项、第4项分别相等。若数列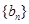 的前
的前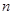 项和
项和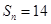 ,求
,求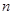 的值。
的值。
在△ 中,内角
中,内角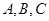 的对边分别为
的对边分别为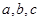 。已知
。已知 ,
, 。(1)求
。(1)求 ;(2)若
;(2)若 ,求△
,求△ 的面积。
的面积。
已知 ,且
,且 ,
,
求:(1) ;
;
(2) ;
;
(3) 的值。
的值。