已知椭圆 过点
过点 ,椭圆
,椭圆 左右焦点分别为
左右焦点分别为 ,上顶点为
,上顶点为 ,
, 为等边三角形.定义椭圆C上的点
为等边三角形.定义椭圆C上的点 的“伴随点”为
的“伴随点”为 .
.
(1)求椭圆C的方程;
(2)求 的最大值;
的最大值;
(3)直线l交椭圆C于A、B两点,若点A、B的“伴随点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.椭圆C的右顶点为D,试探究ΔOAB的面积与ΔODE的面积的大小关系,并证明.
(本小题满分13分)
已知椭圆的中点在原点O,焦点在x轴上,点 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且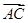 ·
· ="0," |
="0," |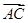 |=|
|=| |.(点C在x轴上方)
|.(点C在x轴上方)
(I)求椭圆的方程;
(II)若平行于CO的直线 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.
设函数 .
.
(Ⅰ)求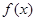 的最小值
的最小值 ;
;
(Ⅱ)若 对
对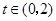 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分) 已知数列 的前
的前 项和为
项和为 ,且
,且 .数列
.数列 满足
满足 (
( ),且
),且 ,
, .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求使不等式
,求使不等式 对一切
对一切 都成立的最大正整数
都成立的最大正整数 的值;
的值;
(本小题满分12分)如图,直角梯形ACDE与等腰直角 所在平面互相垂直,F为BC的中点,
所在平面互相垂直,F为BC的中点, ,
,
(1)求证:平面
(2)求证:
(3)求四面体B-CDE的体积。
(本小题满分12分)某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组。
(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;
(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;
(3)实验结束后,第一次做实验的职员得到的实验数据为68,70,71,72,74,第二次做实验的职员得到的实验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由。