已知斜三棱柱 —
— ,侧面
,侧面 与底面
与底面 垂直,∠
垂直,∠ ,
, ,且
,且 ⊥
⊥ ,
, =
= .
.
(1)试判断 与平面
与平面 是否垂直,并说明理由;
是否垂直,并说明理由;
(2)求侧面 与底面
与底面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【原创】(本小题满分12分)已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在
在 上的最大值与最小值.
上的最大值与最小值.
(本小题满分12分)设 到定点
到定点 的距离和它到直线
的距离和它到直线 距离的比是
距离的比是 .
.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为 的直线过
的直线过 点,且与点
点,且与点 的轨迹交于点
的轨迹交于点 ,
, ,若
,若 ,求△
,求△ 的面积.
的面积.
【原创】(本小题满分13分)已知函数 ,
,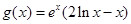 .
.
(Ⅰ)若函数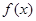 在定义域上是增函数,求a的取值范围;
在定义域上是增函数,求a的取值范围;
(Ⅱ)求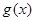 的最大值.
的最大值.
【改编】(本小题满分13分)已知F1、F2分别为椭圆C: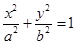 (a>b>0)的左、右焦点, 且离心率为
(a>b>0)的左、右焦点, 且离心率为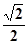 ,点
,点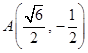 在椭圆C上.
在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在斜率为k的直线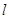 与椭圆C交于不同的两点M、N,使直线
与椭圆C交于不同的两点M、N,使直线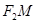 与
与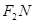 的倾斜角互补,且直线
的倾斜角互补,且直线 是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
(本小题满分12分)已知数列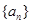 是等差数列,且
是等差数列,且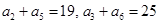 .
.
(Ⅰ)求数列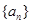 的通项公式;
的通项公式;
(Ⅱ)若数列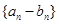 是首项为2,公比为2的等比数列,求数列
是首项为2,公比为2的等比数列,求数列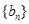 的前
的前 项和
项和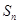 .
.