已知椭圆
的长轴长为
，离心率为
，
分别为其左右焦点．一动圆过点
，且与直线
相切．
（1）求椭圆
及动圆圆心轨迹
的方程；
（2） 在曲线上有两点
、
，椭圆上有两点
、
，满足
与
共线，
与
共线，且
，求四边形
面积的最小值．
用长为90cm，宽为48cm的长方形铁皮做一个无盖的容器，先在四角分别截去一个小正方形，然后把四边翻折900角，再焊接而成，问该容器的高为多少时，容器的容积最大？最大的容积是多少？
已知某几何体的三视图如图，其中正（侧）视图上部为正三角形，下部为矩形，俯视图是正方形.
（1）画出该几何体的直观图(6分)
（2）求该几何体的表面积和体积.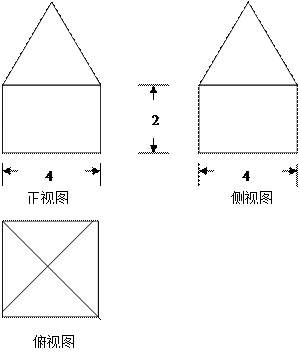
在△ABC中，角A、B、C所对的边分别是a、b、c，且
（1）求
的值；
（2）若
的值
已知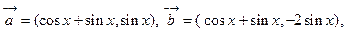
（1）求
的解析式，并用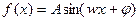
的形式表示
（2）当0≤x≤
时，求此函数的最值及此时的x值.
（本小题满分14分）函数
.
（1）若函数
内单调递增，求a的取值范围；
（2）求函数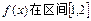
上的最小值.