如图,在平面直角坐标系中,一次函数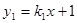 的图象与
的图象与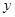 轴交于点A,与
轴交于点A,与 轴交于点B,与反比例函数
轴交于点B,与反比例函数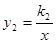 的图象分别交于点M、N,已知△AOB的面积为1,点M的纵坐标为2.
的图象分别交于点M、N,已知△AOB的面积为1,点M的纵坐标为2.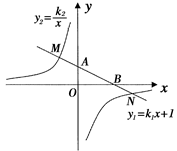
(1)求一次函数与反比例函数的解析式;
(2)直接写出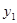 >
>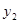 时,
时, 的取值范围.
的取值范围.
已知 ,
, ,
, 是16的平方根,求:
是16的平方根,求: 的值.
的值.
如图所示, 在正方形网格中,若点
在正方形网格中,若点 的坐标为
的坐标为 ,按要求回答下列问题:
,按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点 和点
和点 的坐标;
的坐标;
(3)作出 关于
关于 轴的对称图形
轴的对称图形 (不用写作法),并写出
(不用写作法),并写出 、
、 、
、 的坐标.
的坐标.
如图,在△ADF与△CBE中,点A 、E、F、C在同一直线上,已知AD∥BC,AD=CB,∠B=∠D.求证:AF=CE.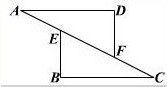
计算:
25、为了美化博望中学校园环境,建设绿色校园,我校准备对校园中30亩空地进行绿化.绿化采用种植草皮与种植树木两种方式,要求种植草皮与种植树木的面积都不少于10亩,并且种植草皮面积不少于种植树木面积的三分之二.已知种植草皮与种植树木每亩的费用分别为8000元与12000元.
(2)种植草皮的面积为多少时绿化总费用最低,最低费用为多少?