(1)已知正方形ABCD ,点E、F、G、H分别在边AB、BC、CD、DA上,若EG⊥FH,求证EG = FH”(如图1);
(2)如果把条件中的“正方形”改为“长方形”,并设AB =2,BC =3(如图2),试探究EG、FH之间有怎样的数量关系,并证明你的结论;
(3)如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为 (如图3),试求EG的长度。
(如图3),试求EG的长度。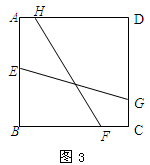
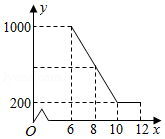
某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元 千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量 (千克)与销售单价 (元 千克)的函数关系如图所示:
(1)求 与 的函数解析式(也称关系式);
(2)求这一天销售西瓜获得的利润 的最大值.
已知 是常数,抛物线 的对称轴是 轴,并且与 轴有两个交点.
(1)求 的值;
(2)若点 在物线 上,且 到 轴的距离是2,求点 的坐标.
如图,四边形 中,对角线 、 相交于点 , , ,且 .
(1)求证:四边形 是矩形;
(2)若 ,求 的度数.

甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用 、 表示.若 为奇数,则甲获胜;若 为偶数,则乙获胜.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,求 所有可能出现的结果总数;
(2)你认为这个游戏对双方公平吗?请说明理由.
为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动.已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.