如图，抛物线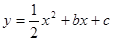
与x轴的两个交点A、B，与y轴交于点C，A点坐标为（4，0），C点坐标（0，－4）．
（1）求抛物线的解析式；
（2）用直尺和圆规作出△ＡＢＣ的外接圆⊙M，（不写作法，保留作图痕迹），并求⊙M的圆心M的坐标；
如图：（1）将△ABO向右平移4个单位，画出平移后的图形．
（2）求△ABO的面积．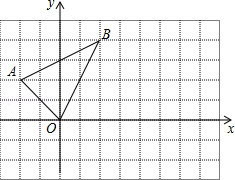
（1）
（2）
．
已知平行四边形ABCD位置在平面直角坐标系中如图1所示，BC=AC，且OA=6，OC=8．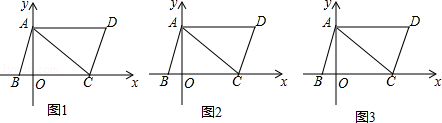
（1）求点D的坐标；
（2）动点P从点C出发，以每秒1个单位的速度沿线段以向终点A运动，动点Q从点A出发以每秒2个单位的速度沿4射线AD运动，两点同时出发，当P到达终点时，点Q停止运动，在运动过程中，过点Q作MQ∥AB交射线AC于M（如图2）．设PM=y，运动时间为t（t＞0），求y与t的函数关系式，并直接写出自变量的取值范围；
（3）在（（2）的条件下，作点P关于直线CD的对称点P′（如图3），当P′D=
时，求运动时间t．
已知：如图，在▱ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．
（1）求证：△DOE≌△BOF；
（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．
八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
| 甲 |
7 |
8 |
9 |
7 |
10 |
10 |
9 |
10 |
10 |
10 |
| 乙 |
10 |
8 |
7 |
9 |
8 |
10 |
10 |
9 |
10 |
9 |
（1）甲队成绩的中位数是 分，乙队成绩的众数是 分；
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1.4分2，则成绩较为整齐的是 队．