如图, 已知抛物线经过坐标原点O及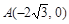 ,其顶点为B(m,3),C是AB中点,
,其顶点为B(m,3),C是AB中点,
点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上, 且EO=ED .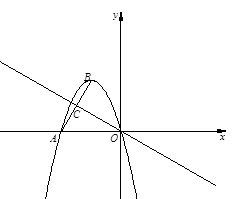
(1)求此抛物线及直线OC的解析式;
(2)当点E运动到抛物线上时,
 求BD的长;
求BD的长;(3)连接AD, 当点E运动到何处时,△AED的面积为
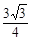 ,请直接写出此时E点的
,请直接写出此时E点的
坐标.
已知在□ABCD中,AE^BC于E,DF平分ÐADC 交线段AE于F.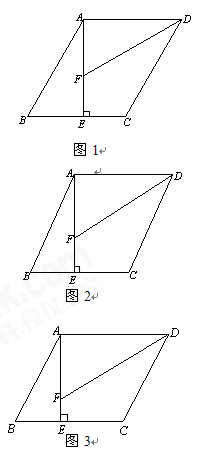
(1)如图1,若AE=AD,ÐADC=60°, 请直接写出线段CD与AF+BE之间所满足的
等量关系;(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论
加以证明, 若不成立, 请说明理由;(3)如图3, 若AE :AD =a :b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你的结论.
已知二次函数y=ax2+bx+c的图象与反比例函数 的图象交于点A (a, -3),与y轴交于点B.
的图象交于点A (a, -3),与y轴交于点B.
(1)试确定反比例函数的解析式;
(2)若ÐABO =135°, 试确定二次函数的解析式;
(3)在(2)的条件下,将二次函数y=ax2 + bx + c的图象先沿x轴翻折, 再向右平移到与反比例函数
 的图象交于点P (x0, 6) . 当x0≤x≤3时, 求平移后的二次函数y的取值范围.
的图象交于点P (x0, 6) . 当x0≤x≤3时, 求平移后的二次函数y的取值范围.
已知△ABC的面积为a,O、D分别是边AC、BC的中点.(1)画图:在图1中将点D绕点O旋转180°得到点E, 连接AE、CE.
填空:四边形ADCE的面积为;
(2)在(1)的条件下,若F1是AB的中点,F2是AF1的中点,F3是AF2的中点,…,
Fn是AFn -1的中点 (n为大于1的整数), 则△F2CE的面积为;
△FnCE的面积为.
如图,AB是⊙O的直径,点C在⊙O上,CE^AB于E, CD平分ÐECB, 交过点B的射线于D, 交AB于F, 且BC=BD.
(1)求证:BD是⊙O的切线;
(2)若AE="9," CE="12," 求BF的长.