如图,过抛物线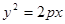 (
( >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标;
⑵求弦AB中点M的轨迹方程。
(本小题满分12分)设函数
(1)写出函数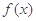 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)当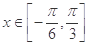 时,函数
时,函数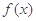 的最大值与最小值的和为
的最大值与最小值的和为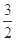 ,求实数
,求实数 的值.
的值.
(本小题满分7分) 选修4—5:不等式选讲
已知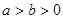 ,且
,且 .
.
(Ⅰ)试利用基本不等式求 的最小值
的最小值 ;
;
(Ⅱ)若实数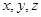 满足
满足 ,求证:
,求证: .
.
(本小题满分7分)选修4—4:极坐标与参数方程
在直角坐标平面内,以坐标原点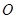 为极点,
为极点,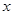 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为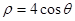 ,直线
,直线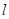 的参数方程为
的参数方程为 (
(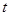 为参数).
为参数).
(Ⅰ)分别求出曲线 和直线
和直线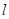 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点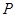 在曲线
在曲线 上,且
上,且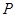 到直线
到直线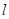 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点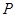 的个数.
的个数.
(本小题满分13分)已知函数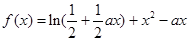 (
( 为常数,
为常数,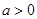 )
)
(1)若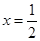 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)求证:当 时,
时, 在
在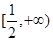 上是增函数;
上是增函数;
(3)若对任意的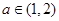 ,总存在
,总存在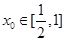 ,使不等式
,使不等式 成立,求正实数
成立,求正实数 的取值范围.
的取值范围.
(本小题满分12分)某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为t件时,销售所得的收入为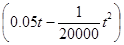 万元.
万元.
(1)该公司这种产品的年生产量为x件,生产并销售这种产品所得到的利润关于当年产量x的函数为f(x),求f(x);
(2)当该公司的年产量为多少件时,当年所获得的利润最大?