如图1,已知有一张三角形纸片ABC的一边AB=10,若D为AB边上的点,过点D作DE//BC交AC于点E,分别过点D、E作DF⊥BC,EG⊥BC,垂足分别为点F、点G,把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠,点A、B、C分别落在A´、B´、C´处.若A´、B´、C´在矩形DFGE内或者其边上,且互不重合,此时我们称△A´B´C´(即图中阴影部分)为“重叠三角形”.
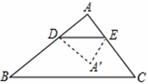
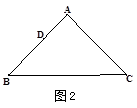
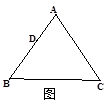
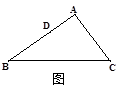

(1)实验操作:当AD=4时,①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”, = ;
= ;
②若AB=AC,BC=12,如图3, = ;③若∠B=30°,∠C=45°,如图4,
= ;③若∠B=30°,∠C=45°,如图4, = ;
= ;
(2)实验探究:若△ABC为等边三角形(如图5),设AD的长为m,若重叠三角形A´B´C´存在,试用含m的代数式表示重叠三角形A´B´C´的面积,并写出m的取值范围.
在 的网格中建立如图的平面直角坐标系,四边形 的顶点坐标分别为 , , , .仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:
(1)将线段 绕点 逆时针旋转 ,画出对应线段 ;
(2)在线段 上画点 ,使 (保留画图过程的痕迹);
(3)连接 ,画点 关于直线 的对称点 ,并简要说明画法.

为改善民生:提高城市活力,某市有序推行"地摊经济"政策.某社区志愿者随机抽取该社区部分居民,按四个类别: 表示"非常支持", 表示"支持", 表示"不关心", 表示"不支持",调查他们对该政策态度的情况,将结果绘制成如图两幅不完整的统计图.根据图中提供的信息,解决下列问题:
(1)这次共抽取了 名居民进行调查统计,扇形统计图中, 类所对应的扇形圆心角的大小是 ;
(2)将条形统计图补充完整;

(3)该社区共有2000名居民,估计该社区表示"支持"的 类居民大约有多少人?
如图直线 分别与直线 , 交于点 , . 平分 , 平分 ,且 .求证: .

计算: .
如图,在平面直角坐标系中,抛物线 的对称轴为直线 ,其图象与 轴交于点 和点 ,与 轴交于点 .
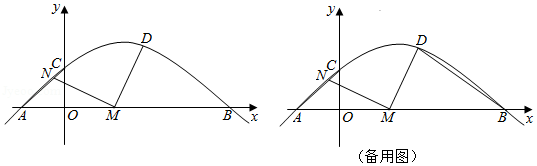
(1)直接写出抛物线的解析式和 的度数;
(2)动点 , 同时从 点出发,点 以每秒3个单位的速度在线段 上运动,点 以每秒 个单位的速度在线段 上运动,当其中一个点到达终点时,另一个点也随之停止运动.设运动的时间为 秒,连接 ,再将线段 绕点 顺时针旋转 ,设点 落在点 的位置,若点 恰好落在抛物线上,求 的值及此时点 的坐标;
(3)在(2)的条件下,设 为抛物线上一动点, 为 轴上一动点,当以点 , , 为顶点的三角形与 相似时,请直接写出点 及其对应的点 的坐标.(每写出一组正确的结果得1分,至多得4分)