如图，点A在x轴负半轴上，点B在y轴正半轴上，线段AB长为6，将线段AB绕A点顺时针旋转60°，B点恰好落在x轴上点D处，点C在第一象限内且四边形ABCD是平行四边形．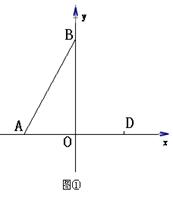
（1）求点C、点D的坐标；
（2）如图②，若半径为1的⊙P从点A出发，沿A—B—D—C以每秒4个单位长的速度匀速移动，同时⊙P的半径以每秒1个单位长的速度匀速增加，当运动到点C时运动停止，运动时间为t秒，试问在整个运动过程中⊙P与y轴有公共点的时间共有几秒？
（3）在（2）的条件下，当⊙P在BD上运动时，过点C向⊙P作一条切线，t为何值时，切线长有最小值，最小值为多少？
先化简，再求值：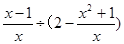 
，其中
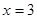
解方程：
如图，在平面直角坐标系中，点C在x的正半轴上，点A在y轴的正半轴上，且OA=7，OC=18，现将点C向上平移7个单位长度再向左平移4单位长度，得到对应点B。
（1）求点B的坐标及四边形ABCO的面积；
（2）若点P从点C以2个单位长度/秒的速度沿CO方向移动，同时点Q从点O以每秒1单位长度的速度沿OA方向移动，设移动的时间为t秒（0<t<7），四边形OPBA与△OQB的面积分别记为S四边形OPBA，S△OQB。
①用含t的式子表示
②是否存在一段时间,使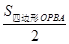 
< S△OQB，若存在，求出t的取值范围，若不存在，试说明理由。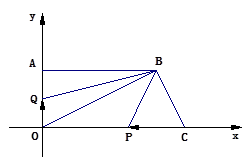 
我县某中学初一年级本学期进行了一次作文比赛，评出一等奖9人，二等奖17人，三等奖14人，学校决定给所有获奖同学各发一份奖品，同一等次的奖品相同.若三种奖品的单价都是整数（以元为单位），且要求一等奖的单价比二等奖的单价多2元，二等奖的单价比三等奖的单价多1元，在总费用不少于200元且不超过250元的前提下，请你列出所有可能的购买方案。
在解方程组
时，由于粗心，甲看错了方程组中的
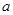，得到的解为
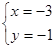；乙看错了方程组中的
，得到的解为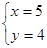
。
（1）求原方程组中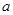、的值各是多少？
（2）求出原方程组中的正确解。