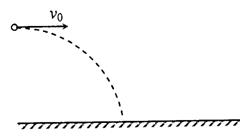
如图所示,一水平光滑、距地面高为h、边长为a的正方形MNPQ桌面上,用长为L的不可伸长的轻绳连接质量分别为mA、mB的A、B两小球,两小球在绳子拉力的作用下,绕绳子上的某点O以不同的线速度做匀速圆周运动,圆心O与桌面中心重合,已知mA=0.5 kg,L=1.2 m,LAO=0.8 m,a=2.1 m,h=1.25 m,A球的速度大小vA=0.4 m/s,重力加速度g取10 m/s2,求: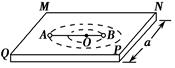
(1)绳子上的拉力F以及B球的质量mB;
(2)若当绳子与MN平行时突然断开,则经过1.5 s两球的水平距离;
(3)两小球落至地面时,落点间的距离.
如图所示,质量为m、电量为q的带电微粒,以初速度V0从A点竖直向上射入水平方向的匀强电场中。当微粒经过B点时速率为VB=2V0,而方向与电场强度方向相同。
求:(1)带电微粒从A运动到B经历的时间
(2)A、B两点间的电势差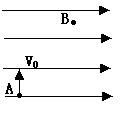
如图所示一束带电粒子(不计重力),垂直电场线方向进入偏转电场,试讨论在以下情况中,粒子应具备什么条件,才能得到相同的偏转距离y和偏转角θ.(U、d、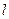 保持不变)
保持不变)
⑴进入偏转电场的速度相同;
⑵进入偏转电场的动能相同;
⑶先静止由同一加速电场加速后,再进入偏转电场.
如图所示,长为2 L的板面光滑且不导电的平板小车C放在光滑水平面上,车的右端有档板,车的质量mC = 4m。今在静止的平板车的左端放一个带电量为+q、质量为m的物块A,在中间位置放一个绝缘物体B,质量为mB=2m。在整个空间加上一个水平方向的匀强电场时,金属块A由静止开始向右运动,并以速度v0与B发生碰撞,碰后A以v0/4的速度反弹回来,B以一定速度沿平板向右运动与C车的档板相碰。碰后小车的速度等于碰前物块B速度的一半。物块A、B均视为质点,A、B相碰时的相互作用力远大于电场力,A和B碰撞时所带电荷量不变。求:
(1)匀强电场的场强大小和方向。
(2)若A第二次与B相碰,判断是在B与C相碰之前还是相碰之后?
(3)A从第一次与B相碰到第二次与B相碰的这段时间内,电场力对A做的功。
游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示。斜
槽轨道AB,EF与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AB,EF分
别与圆O相切于B、E点,C为轨道的最低点,∠BOC=37°。质量为m=0.1kg
的小球从A点静止释放,先后经B、C、D、E到F点落入小框。(整个装置的轨
道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(1)小球在光滑斜槽轨道AB上运动过程中加速度的大小
(2)要使小球从A点到F点的全过程不脱离轨道,A点距离低点的竖直高度h至少多高?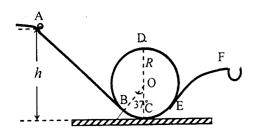
如图所示,在距地面一定高度的地方以初速度v0向右水平抛出一个质量为m,带负电,电量为Q的小球,小球的落地点与抛出点之间有一段相应的水平距离。求:若在空间加上一竖直方向的匀强电场,使小球的水平距离增加为原来的2倍,求此电场场强的大小和方向