已知椭圆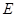
的中心在坐标原点，焦点在
轴上，离心率为
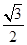，且过双曲线
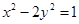的顶点．
（1）求椭圆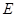的标准方程；
（2）命题：“设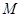
、
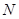是双曲线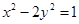上关于它的中心对称的任意两点，
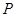为该双曲线上的动点，若直线
、
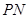均存在斜率，则它们的斜率之积为定值”．试类比上述命题，写出一个关于椭圆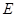的类似的正确命题，并加以证明和求出此定值；
（3）试推广（Ⅱ）中的命题，写出关于方程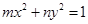
（
，
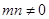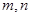不同时为负数）的曲线的统一的一般性命题（不必证明）.
某商场有奖销售中，购满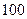
元商品得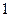
张奖券，多购多得。
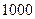张奖券为一个开奖单位，设特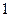等奖个，一等奖
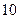个，二等奖
个。设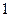张奖券中特等奖、一等奖、二等奖的事件分别为
、
、
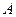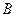，求：
（1）
；
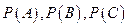（2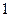）张奖券的中奖概率；
（3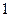）张奖券不中特等奖且不中一等奖的概率。
如图，一面旗帜由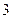
部分构成，这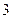部分必须分别着上不同的颜色，现有红、黄、蓝、黑四种颜色可供选择，利用树状图列出所有可能结果，并计算下列事件的概率：
（1）红色不被选中；
（2）第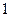
部分是黑色并且第
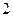部分是红色．
对一批衬衣进行抽检，结果如下表：
（1）完成上面统计表；
（2）事件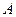
为任取一件衬衣为次品，求
；
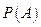（3）为了保证买到次品的顾客能够及时更换，销售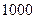
件衬衣，至少需要进货多少件衬衣？
给定整数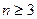
，证明：存在n个互不相同的正整数组成的集合S，使得对S的任意两个不同的非空子集A，B，数
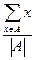与
是互素的合数．（这里
与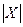
分别表示有限数集
的所有元素之和及元素个数．）
凸
边形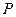
中的每条边和每条对角线都被染为n种颜色中的一种颜色．问：对怎样的n，存在一种染色方式，使得对于这n种颜色中的任何3种不同颜色，都能找到一个三角形，其顶点为多边形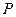的顶点，且它的3条边分别被染为这3种颜色？